Finite Element approximation of
fractional nonlinear PDEs
(joint work with José Carrillo, Endre Süli)
28 March 2025
Universidad Autónoma de Madrid
Partial Differential Equations Seminar
Presentation plan
- The fractional Laplacian
- The fractional porous medium equation
- Finite Element approximation
- Discrete-in-time approximation
- The fractional Keller-Segel model
The fractional Laplacian
What is the classical mathematical operator used to model diffusion?
Standard Laplacian $\Delta = \nabla \cdot \nabla = \frac{\partial^{2}}{\partial x_{1}^{2}} + \dots + \frac{\partial^{2}}{\partial x_{n}^{2}}$
Consider the Fourier Transform for a function $u: \mathbb{R}^{d} \to \mathbb{R}$
$\mathcal{F}[u](\xi) = \hat{u}(\xi) := \int_{\R^{d}} u(x) e^{-2 \pi i\xi \cdot x} dx$
\[ (-\Delta) u(x) \overset{\mathcal{F}}{\longrightarrow} (2 \pi |\xi|)^{2} \hat{u}(\xi) \]
Idea: change the exponent we get out from the action of the Fourier transform
Define the fractional Laplacian as the operator $(-\Delta)^{s}$ such that \[(-\Delta)^{s}u \overset{\mathcal{F}}{\longrightarrow} (2 \pi |\xi|)^{2s} \hat{u} \]
How to give an explicit representation of the fractional Laplacian?
Fractional Laplacian: Singular integral definition
Let $u: \mathbb{R}^{d} \rightarrow \mathbb{R}$, the fractional Laplacian of $u$ is given by \[ \begin{aligned} (-\Delta)^{s}u(x) &= \mathcal{C}(d, s) \; \textup{P.V.} \int_{\mathbb{R}^{d}} \frac{u(x) - u(y)}{|x-y|^{d + 2s}} dy \\ &= \mathcal{C}(d, s) \; \lim_{\epsilon \rightarrow 0} \int_{\mathbb{R}^{d} \setminus B_{\epsilon}} \frac{u(x) - u(y)}{|x-y|^{d + 2s}} dy \end{aligned} \]
Fractional Sobolev space
\[ H^{s}(\Omega) := \bigg \{ u \in L^{2}(\Omega): |u|^{2}_{H^{s}(\Omega)} := \int_{\Omega} \int_{\Omega} \frac{|u(x) - u(y)|^{2}}{|x - y|^{d + 2 s}} \textrm{d}x \, \textrm{d}y < \infty \bigg \}, \] with norm \[ \| u \|_{H^{s}(\Omega)} := \big( \|u\|_{L^{2}(\Omega)}^{2} + |u|^{2}_{H^{s}(\Omega)} \big)^{\frac{1}{2}}. \]
Physical interpretation
Standard Laplacian $\Delta u = \frac{\partial^{2}u}{\partial x_{1}^{2}} + \dots + \frac{\partial^{2}u}{\partial x_{n}^{2}}$
Standard heat equation $\frac{\partial u}{\partial t} = \Delta u$: modelling Brownian motion , continuous version of a standard symmetric random walk

Physical interpretation
Fractional Laplacian $(-\Delta)^{s}u(x) = \mathcal{C}(d, s) \; \textup{P.V.} \int_{\mathbb{R}^{d}} \frac{u(x) - u(y)}{|x-y|^{d + 2s}} dy$
Fractional heat equation $\frac{\partial u}{\partial t} = - (-\Delta)^{s} u$: modelling Lévy walk , continuous version of an energized random walk, allowing long jumps

- Biology: growth of bacteria, movement of antibodies, predator search patterns
- Physics: cristal dislocation, electronagnetic fluids, ground-water solute transport
- Social sciences: human travel
The Fractional Porous medium equation
Porous medium equation
density $\rho = \rho(x, t)$, velocity field $\bm{v} = \bm{v}(x, t)$
\[ \frac{\partial \rho}{\partial t} + \nabla \cdot (\rho \bm{v}) = 0 \]
potential $c= c(x, t)$
\[ \bm{v} = - \nabla c \]
Idea : $ \quad - (-\Delta)^{s} c = \rho$ , $0 < s < 1$
We relate the potential and the density using the fractional Laplacian $(-\Delta)^{s}$
What is the fractional Laplacian?
Spectral fractional Laplacian
Let $\Omega$ be an open, bounded, Lipschitz domain. Let $\{ \psi_{k} \}_{k \geq 1}$ the eigenfunctions of the Laplace operator with a boundary condition $\mathcal{B}(\psi) = 0$, satisfying the eigenvalue problem \[ \left \{ \begin{array}{ll} -\Delta \psi = \lambda \psi & \textrm{in } \Omega, \\ \mathcal{B}(\psi) = 0 & \textrm{on } \partial \Omega. \end{array} \right. \] The spectral fractional Laplacian with boundary condition $\mathcal{B}$ can then be defined by \[ (-\Delta_{\mathcal{B}})^{s} u := \sum_{k=1}^{\infty} \lambda_{k}^{s} u_{k} \psi_{k} \quad \textrm{with } u_{k} = \int_{\Omega} u \psi_{k} \,\text{d}x. \]
Spectral fractional Sobolev space
Let $\Omega$ be an open, bounded, Lipschitz domain. Let $\{ \psi_{k} \}_{k \geq 1}$ the eigenfunctions of the Laplace operator with a boundary condition $\mathcal{B}(\psi) = 0$, satisfying the eigenvalue problem \[ \mathbb{H}^s_{\mathcal{B}}(\Omega) := \Bigg \{ u(\cdot) = \sum_{k=1}^{\infty} u_{k} \psi_{k}(\cdot) \in L^{2}(\Omega): \|u\|^{2}_{\mathbb{H}^s_{\mathcal{B}}(\Omega)} := \sum_{k=1}^{\infty} \lambda_{k}^{s} u_{k}^{2} < \infty \Bigg \} \] \[ \textrm{with } u_{k} := \int_{\Omega} u(x) \psi_{k}(x) \textrm{d}x. \]
What does this give us more in terms of applications?
- Filtration of a fluid through a porous stratum: different pores, tubes and water filaments can make the phenomenon difficult to study $\Rightarrow$ standard models fail in modelling
- Fractional Laplacian models non-local interactions and effects
- More realistic in certain contexts (hydrological setting), where the fluid in the porous medium can contribute to the flux at any point with long jumps
Porous medium equation with a fractional potential
\[ \left \{ \begin{aligned} &\frac{\partial \rho}{\partial t} = \Delta \rho - \nabla \cdot (\rho \nabla c) & \textrm{in } \Omega \times (0, \infty) , \\ & - (-\Delta)^{s} c = \rho^{\ast} = \rho - \int_{\Omega} \rho \, \text{d}x & \textrm{in } \Omega \times (0, \infty), \\ &\partial_{n} \rho = 0, \quad \partial_{n} c = 0 & \textrm{on }\partial \Omega \times (0, \infty). \end{aligned} \right. \]
For us $\Omega$ will be a bounded open polygonal domain in $\mathbb{R}^{2}$ or a bounded open Lipschitz polyhedral domain in $\mathbb{R}^{3}$.
Weak formulation
Let $V = H^{1}(\Omega)$, find $\rho \in L^{2}(0, T; V)$ with $\frac{\partial \rho}{\partial t} \in L^{\infty}(0, T; V')$ such that
\[ \Big\langle \frac{\partial \rho}{\partial t}, \phi \Big\rangle = - \int_{\Omega} \nabla \rho \cdot \nabla \phi + \int_{\Omega} \rho \nabla c \cdot \nabla \phi \quad \text{for all } \phi \in V, \text{ and a. e. } t \in (0, T], \]
where
\[ -(-\Delta_{\mathrm{N}})^{s} c = \rho^{\ast} \textrm{ in } \Omega, \]
subject to the initial condition $\rho(x, 0) = \rho_{0}(x)$, where $\rho_{0} \in L^{\infty}(\Omega)$ and
$\rho_{0}(x) \geq 0$ for a.e. $x \in \Omega$.
Important property : decay in time of the $L^{\infty}$ norm in space
Lemma
Let $\rho$ be a nonnegative strong solution of the fractional porous medium equation and let $F \in C^{2}([0, \infty))$ be convex and let $F(\rho_{0}) \in L^{1}(\Omega)$. Then \[ \frac{d}{dt} \int_{\Omega} F(\rho)\, \text{d}x \leq 0. \]
Corollary
Let $\rho$ be be a nonnegative strong solution of the fractional porous medium equation. The following result holds: \[ \|\rho(t)\|_{L^{\infty}(\Omega)} \leq C \|\rho_{0}\|_{L^{\infty}(\Omega)}. \]
Important property : decay in time for the free energy functional
Let us define \[ G(s) := s(\log s - 1) + 1 \quad \text{for } s > 0 \quad \text{and} \quad G(0):= 1\] and the free energy functional \[ E(\rho) := \int_{\Omega} G(\rho) \, \text{d} x - \frac{1}{2} \int_{\Omega} c \rho \, \text{d}x. \]
Lemma
Let $\rho$ be a nonnegative strong solution of the fractional porous medium equation. Then the following free energy identity holds for all $t\geq 0$ \[ \frac{d}{dt} E(\rho) = - \int_{\Omega} \rho |\nabla (\log \rho - c)|^{2} \, \text{d}x \leq 0 . \]
Regularized weak formualtion
Ingredients :
- cut-off function $\beta_{\delta}^{L}(\cdot)$ with parameters $0< \delta < 1$, $L>1$ \[ \beta_{\delta}^{L}(s) = \left \{ \begin{array}{ll} \delta & s \leq \delta, \\ s & \delta < s < L, \\ L & s \geq L. \end{array} \right. \]
Find $\rho_{\delta, L} \in L^{2}(0, T; V)$ with $\frac{\partial \rho}{\partial t} \in L^{\infty}(0, T; V')$ such that \[ \Big\langle \frac{\partial \rho_{\delta, L}}{\partial t}, \phi \Big\rangle = - \int_{\Omega} \nabla \rho_{\delta, L} \cdot \nabla \phi + \int_{\Omega} \beta_{\delta}^{L}(\rho_{\delta, L}) \nabla c_{\delta, L} \cdot \nabla \phi \quad \text{for all } \phi \in V \quad \text{and a.e. } t \in (0, T], \] where \[ -(-\Delta_{\mathrm{N}})^{s} c = \rho_{\delta, L}^{\ast} \textrm{ in } \Omega, \] subject to the initial condition $\rho_{\delta, L}(x, 0) = \rho_{0}(x)$.
Finite Element approximation
Fractional Porous Medium equation
\[ \left \{ \begin{aligned} &\frac{\partial \rho}{\partial t} = \Delta \rho - \nabla \cdot (\rho \nabla c) & \textrm{in } \Omega \times (0, \infty) , \\ & - (-\Delta)^{s} c = \rho^{\ast} & \textrm{in } \Omega \times (0, \infty), \\ &\partial_{n} \rho = 0, \quad \partial_{n} c = 0 & \textrm{on }\partial \Omega \times (0, \infty). \end{aligned} \right. \]
We want to design a finite element scheme to solve the equation
Finite Element scheme
Ingredients :
- $\mathcal{T}_{h}= \{ K_{n} \}_{n=1}^{M_{h}}$ a quasi-uniform, shape regular and weakly acute triangulation of the domain, $\overline{\Omega} = \cup_{n=1}^{M_{h}} K_{n}$,
- the space of continuous piecewise linear functions
$V_{h} = \{ v_{h} \in C(\overline{\Omega}) \textrm{ such that } v_{h}\big|_{K} \in \mathbb{P}^{1} \textrm{ for all } K \in \mathcal{T}_{h} \}$, - a finite element approximation of the fractional Laplacian
\[ (-\Delta_{h})^{s} u_{h} := \sum_{k=1}^{N_{h}} (\lambda_{k}^{h})^{s} u_{k}^{h} \varphi_{k}^{h} \quad \textrm{with } u_{k}^{h} := \int_{\Omega} u_{h} \varphi_{k}^{h} \,\text{d}x, \] where $\varphi_{k}^{h}$ are the eigenfunctions of the bilinear form $a(\phi, \psi) = \int_{\Omega} \nabla \phi \cdot \nabla \psi \, \text{d}x$ in $V_{h} \cap L^{2}_{\ast}(\Omega)$.
Finite Element scheme
- discrete counterpart of $\beta_{\delta}^{L}(\cdot)$, a diagonal matrix $\Theta_{\delta}^{L}(\phi_{h}) \in \mathbb{R}^{d \times d}$ defined as follows:
for $x \in \Omega$ let $K$ be the element with $x \in K$ and let $\{ P_{i} \}_{i = 0}^{d}$ be the vertices of the simplex; then, for $j = 1, \dots, d$, \[ \widetilde{\Theta}_{\delta}^{L}(\phi_{h})_{jj}(x) = \left \{ \begin{aligned}& \frac{\phi_{h}(P_{j}) - \phi_{h}(P_{0})}{(G_{\delta}^{L})'(\phi_{h}(P_{j})) - (G_{\delta}^{L})'(\phi_{h}(P_{0}))} & \textrm{if } \phi_{h}(P_{j}) \neq \phi_{h}(P_{0}), \\ &\frac{1}{(G_{\delta}^{L})''(\phi_{h}(P_{j}))} = \beta_{\delta}^{L}(\phi_{h}(P_{j})) & \textrm{if } \phi_{h}(P_{j}) = \phi_{0}(P_{j}); \end{aligned} \right. \] let $\widehat{K}$ be the reference simplex and $y \mapsto P_{0} + B_{K} y$ the affine mapping which maps $\widehat{K}$ to $K$, define \[ \Theta_{\delta}^{L}(\phi_{h})(x) = (B_{K}^{\mathrm{T}})^{-1} \widetilde{\Theta}_{\delta}^{L}(\phi_{h})(x) B_{K}^{\mathrm{T}}. \]
Finite Element scheme
\[ \]
Finite Element scheme
Theorem
There exists a subsequence of $\{ \rho_{h, \delta, L}^{n} \}_{\delta, h >0}$ and a nonnegative function $\rho_{L}^{n} \in V$ such that, as $\delta, h \to 0_{+}$ \[ \begin{aligned} \rho_{h, \delta, L}^{n} &\to \rho_{L}^{n} &\text{strongly in} \quad &L^{2}(\Omega), \\ \nabla \rho_{h, \delta, L} &\to \nabla \rho_{L}^{n} & \text{weakly in} \quad &L^{2}(\Omega; \mathbb{R}^{d}), \\ \Theta_{\delta}^{L}(\rho_{h, \delta, L}^{n}) &\to \beta^{L}(\rho^{n}_{L}) I & \text{strongly in} \quad &L^{2}(\Omega; \mathbb{R}^{d \times d}), \\ c_{h, \delta, L}^{n} &\to c_{L}^{n} & \text{strongly in} \quad &L^{2}_{\ast}(\Omega), \\ \nabla c_{h, \delta, L}^{n} &\to \nabla c_{L}^{n} & \text{weakly in} \quad &L^{2}_{\ast}(\Omega; \mathbb{R}^{d}). \end{aligned} \] Moreover $\{ \rho^{n}_{L} \}_{n=1, \dots, N}$ solves a discrete-in-time scheme and given $\rho_{L}^{0}$ such that $\frac{1}{|\Omega|} \int_{\Omega} \rho^{0} \, \text{d}x = 1$, one has $\frac{1}{|\Omega|} \int_{\Omega} \rho^{n}_{L} \, \text{d}x = 1$ for all $n=1, \dots, N$ .
Finite Element scheme
Moreover $\{ \rho^{n}_{L} \}_{n=1, \dots, N}$ solves the discrete-in-time scheme:
For $n = 1, \dots, N$, given $\rho_{L}^{n-1} \in V$ find $\rho_{L}^{n} \in V$ such that \[ \int_{\Omega} \frac{\rho_{L}^{n} - \rho_{L}^{n-1}}{\Delta t} \phi \,\text{d}x = - \int_{\Omega} \nabla \rho_{L}^{n} \cdot \nabla \phi + \int_{\Omega} \beta^{L}(\rho_{L}^{n}) \nabla c_{L}^{n} \cdot \nabla \phi \quad \textrm{for all } \phi \in V, \] where \[ - (-\Delta_{\mathrm{N}})^{s} c_{L}^{n} = (\rho_{L}^{n})^{\ast}, \quad \partial_{n} c_{L}^{n} = 0 \textrm{ on } \partial \Omega \] subject to the initial condition $\rho_{L}^{0} = \rho^{0}$.
Discrete-in-time approximation
Discrete-in-time scheme
Ingredients :
- linear interpolation in time \[ \rho_{L}^{\Delta t}(\cdot, t) := \frac{t - t_{n-1}}{\Delta t} \rho_{L}^{n}(\cdot) + \frac{t_{n} - t}{\Delta t } \rho_{L}^{n-1}(\cdot), \quad t \in [t_{n-1}, t_{n}], \quad n = 1, \dots, N \] \[ \rho_{L}^{\Delta t, +}(\cdot, t) := \rho_{L}^{n}(\cdot), \quad \rho_{L}^{\Delta t, -}(\cdot, t) := \rho_{L}^{n-1}(\cdot), \quad t \in (t_{n-1}, t_{n}), \quad n =1, \dots, N. \]
Discrete-in-time scheme
- uniform bound on $L^{\infty}(\Omega)$ norm of the solution $\rho_{L}^{\Delta t}$, to get rid of the cut-off parameter $L$
Corollary
Let $\rho_{L}^{\Delta t (,\pm)}$ defined as before. The following bound holds: \[ \sup_{t \in [0,T]} \|\rho_{L}^{\Delta t (,\pm)}(t)\|_{L^{\infty}(\Omega)} \leq C \|\rho_{0}\|_{L^{\infty}(\Omega)}. \]
Discrete-in-time scheme
Discrete-in-time scheme
Theorem
There exists a subsequence $\{ \rho^{\Delta t(,\pm)} \}_{\Delta t>0}$ and a function $\widehat{\rho}$ such that \[ \widehat{\rho} \in L^{\infty}(0, T, L^{\infty}(\Omega)) \cap H^{1}(0, T, H^{-\beta}(\Omega)), \quad \beta = d+1, \] with $\widehat{\rho} \geq 0$ almost everywhere on $\Omega \times (0, T)$ and $\frac{1}{|\Omega|} \int_{\Omega} \widehat{\rho}(x, t) \, \text{d}x = 1$ for a.e. $t \in [0, T]$, and a function $\widehat{c}(\cdot, t) \in \mathbb{H}^{s}(\Omega) \cap H^{1}_{\ast}(\Omega)$, defined as $-(-\Delta_{\mathrm{N}})^{s} \widehat{c} = \widehat{\rho}^{\ast}$, such that, for all $p \in [1, \infty)$, as $\Delta t \to 0$, \[ \begin{aligned} \rho^{\Delta t(,\pm)} & \to \widehat{\rho} &\text{strongly in} \quad & L^{p}(0,T;L^{1}(\Omega)), \\ \nabla \sqrt{\rho^{\Delta t(,\pm)}} & \to \nabla \sqrt{\widehat{\rho}} &\text{weakly in} \quad & L^{2}(0,T;L^{2}(\Omega; \mathbb{R}^{d})), \\ \frac{\partial \rho^{\Delta t}}{\partial t} & \to \frac{\partial \widehat{\rho}}{\partial t} &\text{weakly in} \quad & L^{2}(0,T; H^{-\beta}(\Omega)), \\ \rho^{\Delta t(,\pm)} & \to \widehat{\rho} &\text{weakly-$*$ in} \quad & L^{\infty}(0,T;L^{\infty}(\Omega)), \\ \rho^{\Delta t(,\pm)} & \to \widehat{\rho} &\text{strongly in} \quad & L^{p}(0,T;L^{p}(\Omega)), \end{aligned} \]
Discrete-in-time scheme
\[ \begin{aligned} c^{\Delta t(,\pm)} & \to \widehat{c} & \text{strongly in} \quad & L^{p}(0, T; \mathbb{H}^{s}(\Omega)), \\ \nabla c^{\Delta t, +} & \to \nabla \widehat{c} & \text{weakly in} \quad & L^{2}(0, T; L^{2}(\Omega; \mathbb{R}^{d})). \end{aligned} \] Moreover the function $\widehat{\rho}$ is a global weak solution to the problem
\[ \begin{gathered} -\int_{0}^{T} \int_{\Omega} \widehat{\rho} \frac{\partial \phi}{\partial t} \, \text{d}x \, \text{d}t + \int_{0}^{T} \int_{\Omega} \nabla \widehat{\rho} \cdot \nabla \phi \, \text{d}x \, \text{d}t + \int_{0}^{T} \int_{\Omega} \widehat{\rho} \, \nabla \widehat{c} \cdot \nabla \phi \, \text{d}x \, \text{d}t= \int_{\Omega} \rho_{0} \;\phi|_{t=0} \, \text{d}x \\ \text{for all } \phi \in W^{1,1}(0, T; H^{\beta}(\Omega)) \text{ such that } \phi(., T) = 0. \end{gathered} \]
In addition, the function $\widehat{\rho}$ is weak-$*$ continuous as a mapping from $[0,T]$ to $L^{\infty}(\Omega)$ and it is weakly continuous as a mapping from $[0, T]$ to $L^{1}(\Omega)$. The energy functional $E(\cdot)$ satisfies the inequality \[ E(\widehat{\rho}(t)) + \int_{0}^{t} \int_{\Omega} \bigg| 2 \nabla \sqrt{\widehat{\rho}} - \sqrt{\widehat{\rho}} \nabla \widehat{c} \bigg|^{2} \text{d}x \text{d}\tau \leq E(\rho_{0}), \] for a.e. $t \in [0, T]$.
Exponential decay properties
Theorem
$(a)$ For any $T>0$, the functional $G(\cdot)$, exhibits exponential decay, \[ \int_{\Omega} G(\widehat{\rho}(T)) \text{d}x \leq e^{-\frac{2T}{C_{\Omega} \| \rho_{0} \|_{L^{\infty}(\Omega)}}} \int_{\Omega} G(\rho_{0}) \text{d}x. \] $(b)$ The function $\widehat{\rho}$ satisfies the inequality \[ \frac{1}{2 |\Omega|} \| \widehat{\rho}(\cdot, T) - 1 \|_{L^{1}(\Omega)}^{2} \leq e^{-\frac{2T}{C_{\Omega} \| \rho_{0} \|_{L^{\infty}(\Omega)}}} \int_{\Omega} E(\rho_{0}) \text{d}x. \] $(c)$ Assuming in addition that $\Omega$ is convex and that $s \in (1/2, 1)$, the energy functional $E(\cdot)$ exhibits exponential decay, \[ \int_{\Omega} E(\widehat{\rho}(T)) \text{d}x \leq e^{-\frac{8T}{3C_{\Omega} \| \rho_{0} \|_{L^{\infty}(\Omega)}}} \int_{\Omega} E(\rho_{0}) \text{d}x. \]
Consider different initial data $\rho_{0}$ on $\Omega = (0,1)^{2}$, we can check the exponential convergence to equilibrium.
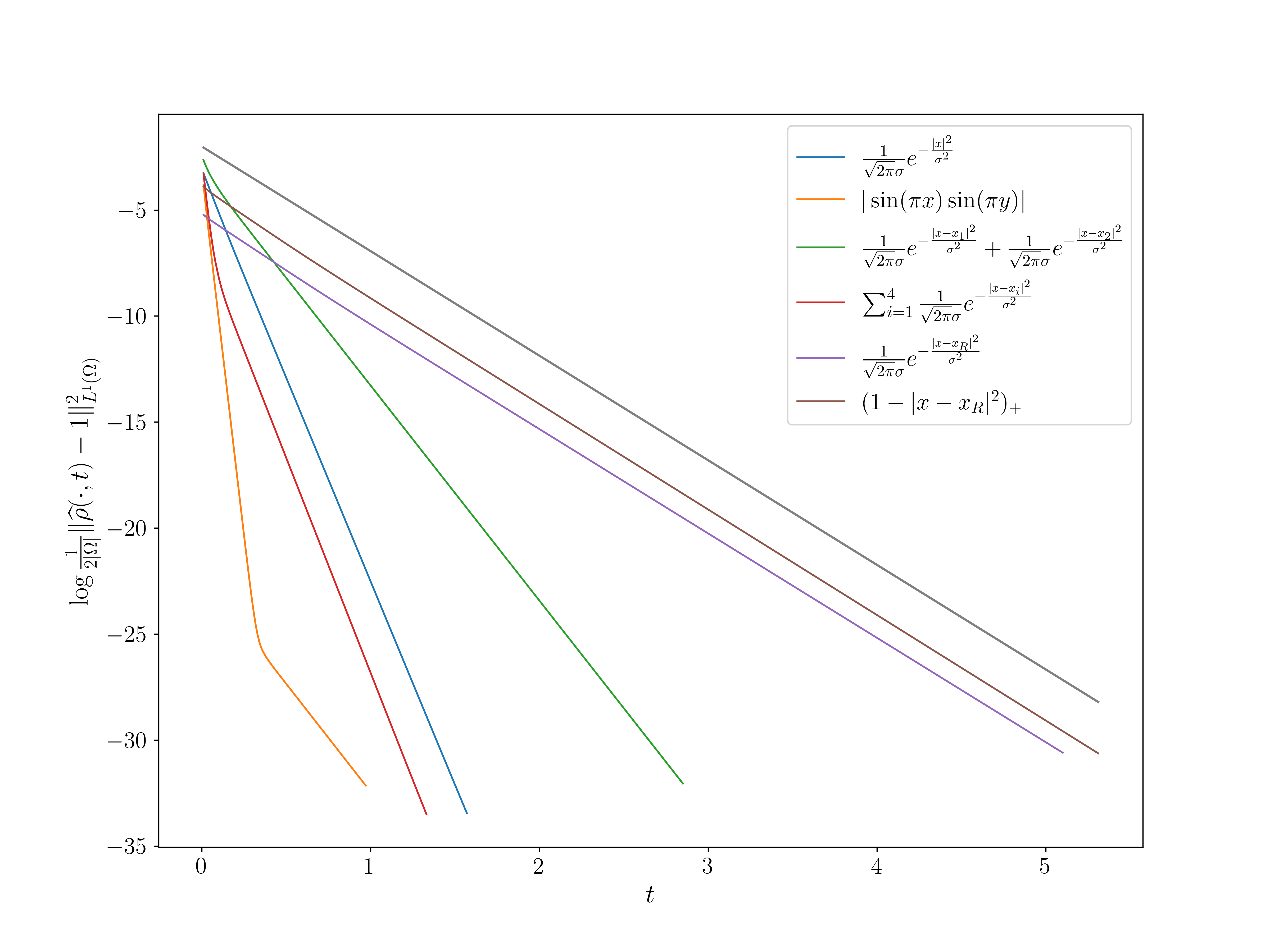
We can get simulations for the fractional porous medium equation for different fractional orders on a large variety of domains, in an efficient and fast way. We can compare different self similar profiles to see the effect of having fractional Laplacian in the potential
central section of 2D simulations
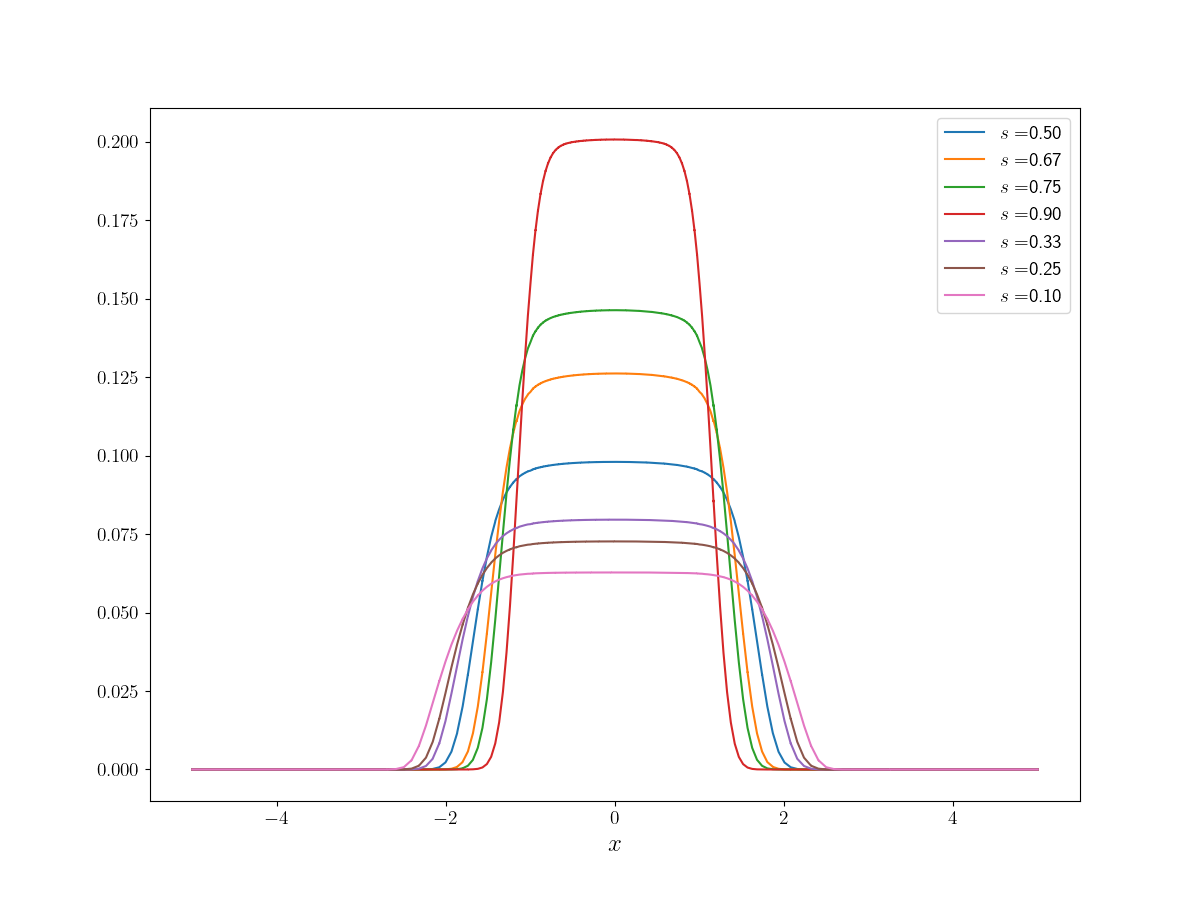
Property: the comparison principle does not hold.
Consider different initial data $u_{1}$ and $u_2$ on $\Omega = (-5,5)^{2}$, initially ordered $u_1 \leq u_2$: for some $c>0$ \[ u_1(x) = \exp(-|x-2|^2/c), \qquad u_2(x) = \exp(-|x-2|^2/c) + 2 \exp(-|x+2|^2/c). \]
Property: the comparison principle does not hold.
Consider different initial data $u_{1}$ and $u_2$ on $\Omega = (-5,5)^{2}$, initially ordered $u_1 \leq u_2$: for some $c>0$ \[ u_1(x) = \exp(-|x-2|^2/c), \qquad u_2(x) = \exp(-|x-2|^2/c) + 2 \exp(-|x+2|^2/c). \]
diagonal section
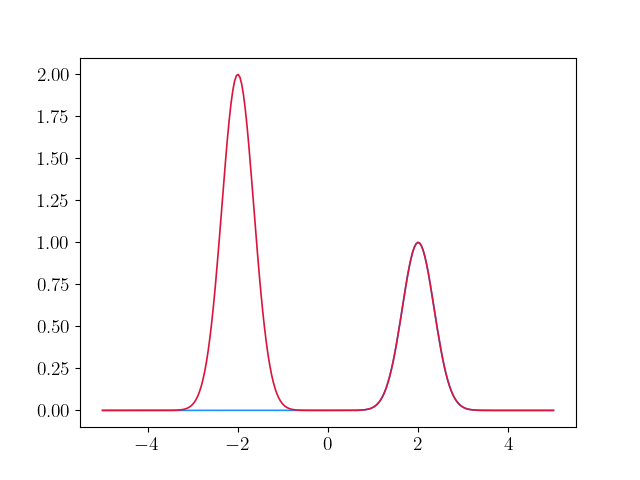
Property: the comparison principle does not hold.
Consider different initial data $u_{1}$ and $u_2$ on $\Omega = (-5,5)^{2}$, initially ordered $u_1 \leq u_2$: for some $c>0$ \[ u_1(x) = \exp(-|x-2|^2/c), \qquad u_2(x) = \exp(-|x-2|^2/c) + 2 \exp(-|x+2|^2/c). \]

Property: the comparison principle does not hold.
Consider different initial data $u_{1}$ and $u_2$ on $\Omega = (-5,5)^{2}$, initially ordered $u_1 \leq u_2$: for some $c>0$ \[ u_1(x) = \exp(-|x-2|^2/c), \qquad u_2(x) = \exp(-|x-2|^2/c) + 2 \exp(-|x+2|^2/c). \]
central section
The fractional Keller-Segel model
Fractional Porous Medium equation
\[ \left \{ \begin{aligned} &\frac{\partial \rho}{\partial t} = \Delta \rho - \nabla \cdot (\rho \nabla c) & \textrm{in } \Omega \times (0, \infty) , \\ & - (-\Delta)^{s} c = \rho^{\ast} & \textrm{in } \Omega \times (0, \infty), \\ &\partial_{n} \rho = 0, \quad \partial_{n} c = 0 & \textrm{on }\partial \Omega \times (0, \infty). \end{aligned} \right. \]
Question : what if the same potential becomes attractive ?
Fractional Keller-Segel equation
\[ \left \{ \begin{aligned} &\frac{\partial \rho}{\partial t} = \Delta \rho - \nabla \cdot (\rho \nabla c) & \textrm{in } \Omega \times (0, \infty) , \\ & (-\Delta)^{s} c = \rho^{\ast} & \textrm{in } \Omega \times (0, \infty), \\ &\partial_{n} \rho = 0, \quad \partial_{n} c = 0 & \textrm{on }\partial \Omega \times (0, \infty). \end{aligned} \right. \]
It is well know that blow-up of the solution can occurr.
For standard Keller-Segel ($s=1$) on $\mathbb{R}^{2}$ the blow-up depends only on the initial mass of the solution $M = \int_{\mathbb{R}^{d}} \rho_{0} \, \text{d}x$: \[ M < 8 \pi \Longrightarrow \text{NO blow-up} \] \[ M > 8 \pi \Longrightarrow \text{blow-up} \]
Fractional Keller-Segel equation
\[ \left \{ \begin{aligned} &\frac{\partial \rho}{\partial t} = \Delta \rho - \nabla \cdot (\rho \nabla c) & \textrm{in } \Omega \times (0, \infty) , \\ & (-\Delta)^{s} c = \rho^{\ast} & \textrm{in } \Omega \times (0, \infty), \\ &\partial_{n} \rho = 0, \quad \partial_{n} c = 0 & \textrm{on }\partial \Omega \times (0, \infty). \end{aligned} \right. \]
For fractional Keller-Segel ($s \in (0,1)$) it is know that the blow-up depends not only on the initial mass of the solution $M = \int_{\mathbb{R}^{d}} \rho_{0} \, \text{d}x$, but also on its initial concentration $\int_{\mathbb{R}^{d}} |x|^{2} \rho \, \text{d}x$ (P. Biler and W. A. Woyczynski. "Global and Exploding Solutions for Nonlocal Quadratic Evolution Problems".)
We would like to investigate numerically this model and its features.
Consider the unit ball $\Omega = B(0, 1) \subset \mathbb{R}^{2}$, $s = 3/4$ and different initial data, $\rho_{0} \propto e^{-\frac{|x|^{2}}{2\sigma}}$ Gaussians with different initial mass $M$ and different concentration $\sigma$. We study blow-up (orange cell) and no blow-up (green cell).

Consider the unit ball $\Omega = B(0, 1) \subset \mathbb{R}^{2}$, $s = 3/4$ and different initial data, $\rho_{0} \propto e^{-\frac{|x|^{2}}{2\sigma}}$ Gaussians with same initial mass $M=4\pi$ and different concentration $\sigma$. We look to the evolution in time of the $\max( \| \rho \|_{L^\infty(\Omega)}, |\rho|_{H^1(\Omega)} )$ norm of the solution and its second moment.
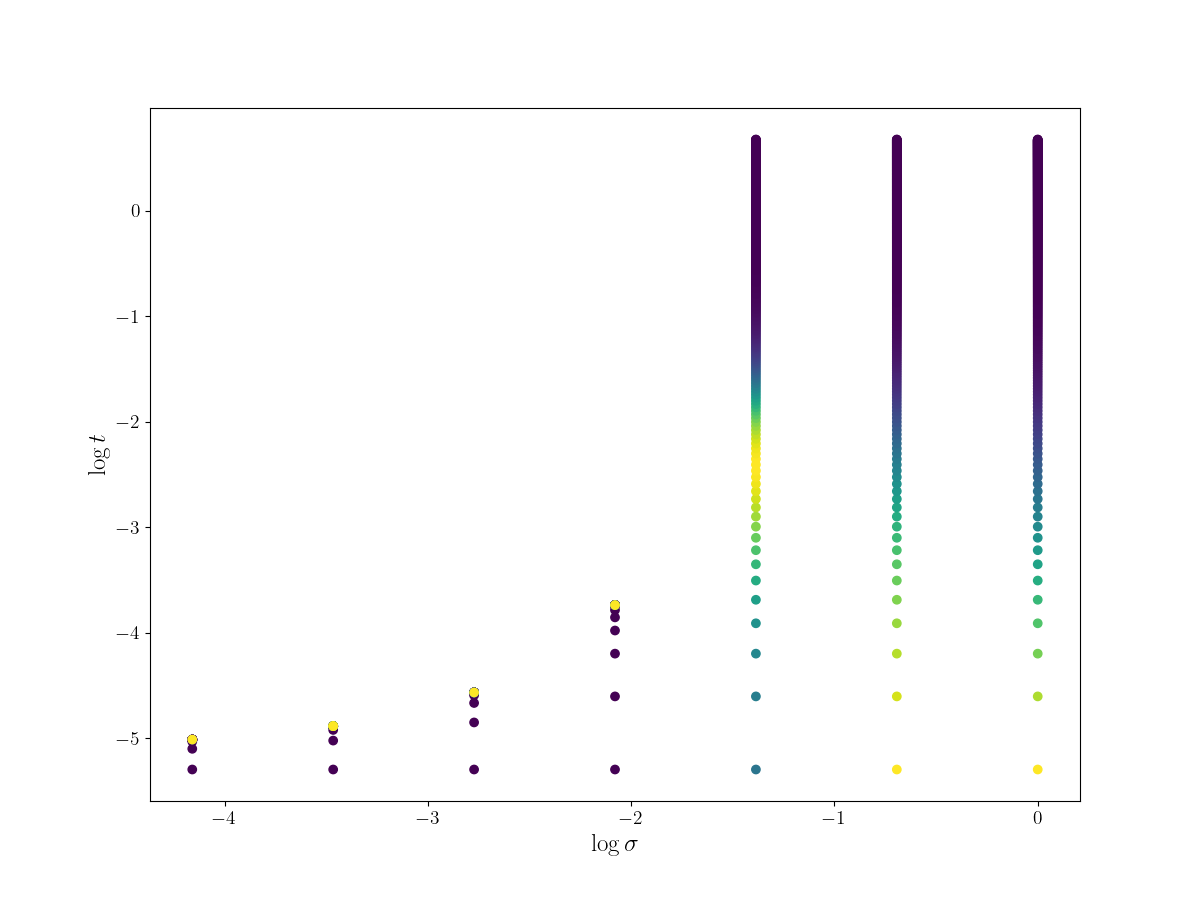
Consider the unit ball $\Omega = B(0, 1) \subset \mathbb{R}^{2}$, we can explore the baheviour of the model taking a lower fractional order $s = 1/2 + \varepsilon$ and different initial data, Gaussians with different initial mass $M$ and different concentration $\sigma$. We study blow-up (orange cell) and no blow-up (green cell).

Thank you for the attention
If you want to know more...
